📃 문제: 백준 1300(K번째 수)
1300번: K번째 수
세준이는 크기가 N×N인 배열 A를 만들었다. 배열에 들어있는 수 A[i][j] = i×j 이다. 이 수를 일차원 배열 B에 넣으면 B의 크기는 N×N이 된다. B를 오름차순 정렬했을 때, B[k]를 구해보자. 배열 A와 B
www.acmicpc.net
세준이는 크기가 N×N인 배열 A를 만들었다. 배열에 들어있는 수 A[i][j] = i×j 이다. 이 수를 일차원 배열 B에 넣으면 B의 크기는 N×N이 된다. B를 오름차순 정렬했을 때, B[k]를 구해보자.
배열 A와 B의 인덱스는 1부터 시작한다.
[입력] 첫째 줄에 배열의 크기 N이 주어진다. N은 105보다 작거나 같은 자연수이다. 둘째 줄에 k가 주어진다. k는 min(109, N2)보다 작거나 같은 자연수이다.
[출력]
B[k]를 출력한다.
🥇 난이도: 골드 1
( 나에겐 어렵다...ㅇㅁㅇ; )
😲 사용한 개념: 이진탐색
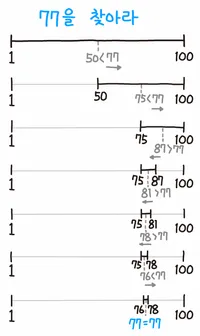
이진탐색은 정렬된 데이터에서 수행할 수 있는 효율적인 탐색 알고리즘으로 O(logN)의 시간복잡도를 갖는다.
중간값을 기준으로, (찾고자 하는 값)<(중간값)이면, 중간값의 오른쪽에 위치한 값을 제외한 범위내에서 다시 탐색을 수행하고, (찾고자 하는 값)>(중간값)이라면, 중간값의 왼쪽에 위치한 값을 제외한 범위 내에서 다시 탐색을 수행하며, (찾고자 하는 값) = (중간값)이 되면 탐색을 종료한다.
탐색을 한바퀴 수행할 때마다 탐색 범위가 절반으로 줄기 때문에, O(logN)의 시간복잡도를 갖는다.
ex) 탐색 범위가 16이라면,
탐색 한바퀴 -> 탐색범위 8개
탐색 두바퀴 -> 탐색범위 4개
탐색 세바퀴 -> 탐색범위 2개
탐색 4바퀴 -> 남은 원소 1개
즉, log2(밑)16 = log2(밑)2^4 의 시간 복잡도를 갖게 되는 것이다.
📖 풀이 사고 과정


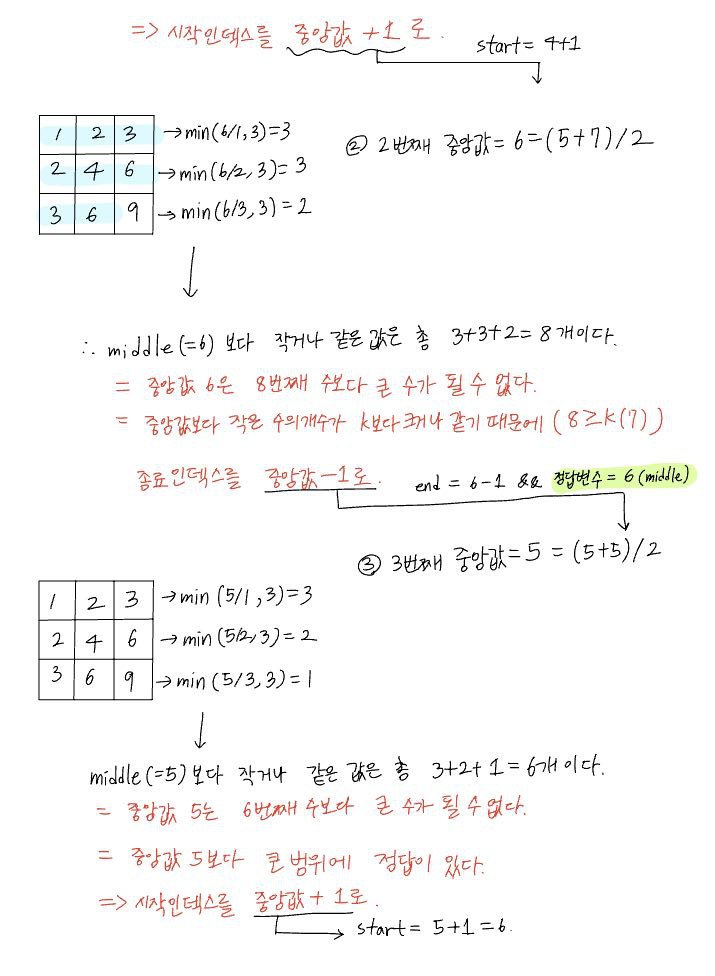

👩💻 구현 코드(c++ 사용)
#include <iostream>
using namespace std;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
long N, K, answer=0, middle;
cin >> N >> K;
//시작 인덱스, 종료 인덱스 초기화
long start = 1, end = K;
while (start <= end) {
middle = (start + end) / 2;
long cnt = 0;
//중앙값(middle)보다 작은 수 몇개인지 카운트
for (int i = 1; i <= N; i++) {
cnt += min(middle/i, N);
}
if (cnt < K) {
start = middle + 1;
}
else {
answer = middle;
end = middle - 1;
}
}
cout << answer << endl;
return 0;
}'백준' 카테고리의 다른 글
| 백준 1715: 카드 정렬하기 (0) | 2024.03.13 |
|---|---|
| 백준 11047: 동전 0 (0) | 2024.02.18 |
| 백준 2805: 나무 자르기 (1) | 2024.02.15 |
| 백준 1920: 수 찾기 (1) | 2024.02.11 |
| 백준 1167: 트리의 지름 (0) | 2024.02.08 |



