📃 문제: 백준 1920(수 찾기)
1920번: 수 찾기
첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들
www.acmicpc.net
N개의 정수 A[1], A[2], …, A[N]이 주어져 있을 때, 이 안에 X라는 정수가 존재하는지 알아내는 프로그램을 작성하시오.
[입력] 첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들이 A안에 존재하는지 알아내면 된다. 모든 정수의 범위는 -231 보다 크거나 같고 231보다 작다.
[출력] M개의 줄에 답을 출력한다. 존재하면 1을, 존재하지 않으면 0을 출력한다.
🥈 난이도: 실버 4
😲 사용한 개념: 이진탐색
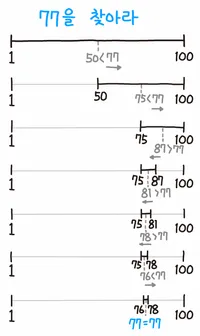
이진탐색은 정렬된 데이터에서 수행할 수 있는 효율적인 탐색 알고리즘으로 O(logN)의 시간복잡도를 갖는다.
중간값을 기준으로, (찾고자 하는 값)<(중간값)이면, 중간값의 오른쪽에 위치한 값을 제외한 범위내에서 다시 탐색을 수행하고, (찾고자 하는 값)>(중간값)이라면, 중간값의 왼쪽에 위치한 값을 제외한 범위 내에서 다시 탐색을 수행하며, (찾고자 하는 값) = (중간값)이 되면 탐색을 종료한다.
탐색을 한바퀴 수행할 때마다 탐색 범위가 절반으로 줄기 때문에, O(logN)의 시간복잡도를 갖는다.
ex) 탐색 범위가 16이라면,
탐색 한바퀴 -> 탐색범위 8개
탐색 두바퀴 -> 탐색범위 4개
탐색 세바퀴 -> 탐색범위 2개
탐색 4바퀴 -> 남은 원소 1개
즉, log2(밑)16 = log2(밑)2^4 의 시간 복잡도를 갖게 되는 것이다.
📖 풀이 사고 과정

👩💻 구현 코드(c++ 사용)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, M;
cin >> N;
vector<int> total(N);
for (int i = 0; i < N; i++) {
cin >> total[i];
}
//전체 배열 오름차순 정렬(이진탐색 수행을 위해)
sort(total.begin(), total.end());
cin >> M;
int target;
for (int i = 0; i <M; i++) {
bool exist = false;
cin >> target;
int start = 0, end = N-1;//시작~끝 인덱스 범위
while (start<=end) {
int middle = (start + end) / 2;
if (target < total[middle]) end = middle - 1;
else if (target > total[middle])start = middle + 1;
else if(target==total[middle]) {
exist = true;
break;
}
}
if (exist) cout << "1" << endl;
else cout << "0" << endl;
}
return 0;
}
👿👿👿
(╯°□°)╯︵ ┻━┻
알고리즘 분류에 '이분탐색'으로 되어있고, 계산해봤을 때 이분탐색으로 풀면 시간초과가 안난다고 생각했는데 자꾸 시간초과가 나서 결국 다른 방법으로 풀었다. 자료구조 set을 이용한 방법은 밑에 기록해두었다.
🎯자료구조 std::set에 대하여
보다시피 std::set은 균형 이진 탐색 트리를 사용하여, 데이터를 항상 정렬된 상태로 유지한다.
디버깅 화면을 보았을 때, 무작위로 입력받은 수를 오름차순으로 set 자료구조에 저장하는 것을 확인할 수 있다.
이로 인해 find, insert, erase 등의 연산이 시간 내에 수행된다.

🎯find 함수에 대하여
Visual C++에서 set::find 함수 사용 - Visual C++
Visual C++에서 set::find STL 함수를 사용하는 방법을 설명합니다. 이 문서에는 샘플 코드가 포함되어 있습니다.
learn.microsoft.com
찾는 값이 있는 경우, 첫번째로 일치하는 원소를 가리키는 iterator를 리턴한다.
일치하는 원소가 없는 경우, last 가 리턴된다.
👩💻 구현 코드(c++ 사용)
#include <iostream>
#include <set>
using namespace std;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N, M, temp;
cin >> N;
set<int> total;
for (int i = 0; i < N; i++) {
cin >> temp;
total.insert(temp);
}
cin >> M;
for (int i = 0; i < M; i++) {
cin >> temp;
cout << (total.find(temp) != total.end() ? "1\n" : "0\n");
}
return 0;
}'백준' 카테고리의 다른 글
| 백준 1300: K번째 수 (1) | 2024.02.17 |
|---|---|
| 백준 2805: 나무 자르기 (1) | 2024.02.15 |
| 백준 1167: 트리의 지름 (0) | 2024.02.08 |
| 백준 2178: 미로 탐색 (0) | 2024.02.08 |
| 백준 1260: DFS와 BFS (1) | 2024.02.06 |



