📃 문제: 백준 2805(나무 자르기)
2805번: 나무 자르기
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) 둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보
www.acmicpc.net
상근이는 나무 M미터가 필요하다. 근처에 나무를 구입할 곳이 모두 망해버렸기 때문에, 정부에 벌목 허가를 요청했다. 정부는 상근이네 집 근처의 나무 한 줄에 대한 벌목 허가를 내주었고, 상근이는 새로 구입한 목재절단기를 이용해서 나무를 구할것이다.
목재절단기는 다음과 같이 동작한다. 먼저, 상근이는 절단기에 높이 H를 지정해야 한다. 높이를 지정하면 톱날이 땅으로부터 H미터 위로 올라간다. 그 다음, 한 줄에 연속해있는 나무를 모두 절단해버린다. 따라서, 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다. 예를 들어, 한 줄에 연속해있는 나무의 높이가 20, 15, 10, 17이라고 하자. 상근이가 높이를 15로 지정했다면, 나무를 자른 뒤의 높이는 15, 15, 10, 15가 될 것이고, 상근이는 길이가 5인 나무와 2인 나무를 들고 집에 갈 것이다. (총 7미터를 집에 들고 간다) 절단기에 설정할 수 있는 높이는 양의 정수 또는 0이다.
상근이는 환경에 매우 관심이 많기 때문에, 나무를 필요한 만큼만 집으로 가져가려고 한다. 이때, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.
[입력]
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000)
둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보다 크거나 같기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다. 높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다.
[출력]
적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.
🥈 난이도: 실버 2
😲 사용한 개념: 이진탐색
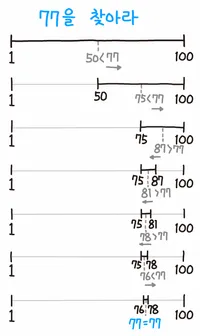
이진탐색은 정렬된 데이터에서 수행할 수 있는 효율적인 탐색 알고리즘으로 O(logN)의 시간복잡도를 갖는다.
중간값을 기준으로, (찾고자 하는 값)<(중간값)이면, 중간값의 오른쪽에 위치한 값을 제외한 범위내에서 다시 탐색을 수행하고, (찾고자 하는 값)>(중간값)이라면, 중간값의 왼쪽에 위치한 값을 제외한 범위 내에서 다시 탐색을 수행하며, (찾고자 하는 값) = (중간값)이 되면 탐색을 종료한다.
탐색을 한바퀴 수행할 때마다 탐색 범위가 절반으로 줄기 때문에, O(logN)의 시간복잡도를 갖는다.
ex) 탐색 범위가 16이라면,
탐색 한바퀴 -> 탐색범위 8개
탐색 두바퀴 -> 탐색범위 4개
탐색 세바퀴 -> 탐색범위 2개
탐색 4바퀴 -> 남은 원소 1개
즉, log2(밑)16 = log2(밑)2^4 의 시간 복잡도를 갖게 되는 것이다.
📖 풀이 사고 과정


⚠️ 구현 시 유의할 점
입력 예시를 입력했을 때 출력은 동일하게 나오고, 구현 로직도 올바르게 짠 것 같은데
계속 틀렸습니다가 나와 헤맸다.
알고보니 입력받는 N, M의 범위가 매우 커서 (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) 변수를 선언할 때
int형으로는 오버플로우가 발생하는 경우가 생겨 통과를 못했던 것이었다!
👉int 형은 4byte로,
| -2,147,483,648 ~ 2,147,483,647 |
해당 범위 값을 가지는데, 절단기로 자른 나무 길이의 합을 구할 때 해당 범위를 넘어가 오버플로우가 발생하는 경우가 생길 수 있다.
데이터 형식 범위
자세한 정보: 데이터 형식 범위
learn.microsoft.com
이런 사소하지만 중요한 지점들을 놓치지 않고 꼼꼼히 조건을 확인해야 함을 다시 한번 느꼈다.
👩💻 구현 코드(c++ 사용)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
//나무의 높이나 요구되는 나무 길이의 합계가 'int' 범위를 초과할 수 있으므로,
//int가 아닌 long long 타입으로 선언하기
long long startPoint, endPoint, middle, sum=0;
long long H, minTreeLength, N;
vector<int> trees;
//H: 절단기 높이
long long treeLength(int H) {
long long sum = 0;
for (int i = 0; i < N; i++) {
if (trees[i] > H) {
sum += (trees[i] - H);
}
}
return sum;
}
int main(void) {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N>>minTreeLength;
trees.resize(N);
for (int i = 0; i < N; i++) {
cin >> trees[i];
}
//start, end 초기화
startPoint = 0;
endPoint = *max_element(trees.begin(), trees.end());
long long optimalHeight=0;
while (startPoint <= endPoint) {
//절단기의 높이
middle = (startPoint + endPoint) / 2;
if (minTreeLength <= treeLength(middle)) {
optimalHeight = middle;
startPoint = middle + 1;
}
else if (minTreeLength > treeLength(middle)) {
endPoint = middle - 1;
}
}
cout << optimalHeight << endl;
return 0;
}
'백준' 카테고리의 다른 글
| 백준 11047: 동전 0 (0) | 2024.02.18 |
|---|---|
| 백준 1300: K번째 수 (1) | 2024.02.17 |
| 백준 1920: 수 찾기 (1) | 2024.02.11 |
| 백준 1167: 트리의 지름 (0) | 2024.02.08 |
| 백준 2178: 미로 탐색 (0) | 2024.02.08 |



