Dynamic Programming이란?
알고리즘 문제를 풀이할 때 최적의 해를 구하기에 연산량이 많아서 시간이 많이 필요하거나, 메모리 공간이 많이 필요한 문제들이 있다. 그래서 문제를 풀 때 연산 속도와 메모리 공간을 최대한으로 절약할 수 있게 효율적으로 알고리즘을 작성해야 한다.
이번에 정리할 Dynamic Programming은 메모리 공간을 약간 더 사용하면 연산속도를 비약적으로 증가시킬 수 있는 방법이다. Dynamic Programming의 기본적인 아이디어를 살펴보자.
이 알고리즘은 아래 두가지 조건을 만족할 때 적용할 수가 있다.
1) 큰 문제를 작은 문제로 나눌 수 있는가? -> Yes
2) 작은 문제에서 구한 정답이 그것을 포함하는 큰 문제에도 동일하게 적용되는가? -> Yes
이를 만족하는 대표적인 예시가 '피보나치 수열' 이다.
피보나치 수열은
f(1) = 1, f(2) = 1,
f(3) = f(2) + f(1) = 1 + 1 = 2,
f(4) = f(3) + (2) = 2 + 1 = 3,
f(5) = f(4) + f(3) = 3 + 2 = 5
...
이와 같이 연산이 된다.
앞선 두 항의 합이 현재 항의 값이 되는 형태의 수열이다.
다항식으로 표현하면 an = a(n-1) + a(n-2), a1 = 1, a2 = 1이 된다.
이 피보나치 수열을 계산하는 코드를 작성해본다면....
간결하게 작성하려면 재귀함수를 써서 구현할 수가 있다.
#include <iostream>
#include <ctime>
using namespace std;
// 재귀함수로 구현
int fibonacci(int n) {
if (n == 1 or n == 2) {
return 1;
}
else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
int main(void) {
// 시간 측정용
clock_t start, finish;
double duration;
int n;
cin >> n;
start = clock();
int result = fibonacci(n);
finish = clock();
duration = (double)(finish - start) / CLOCKS_PER_SEC;
cout << "f(" << n << ") = " << result << endl;
cout << "소요시간(sec): " << duration << endl;
return 0;
}
하지만 이렇게 풀면 문제가 있다.
n이 커질수록 연산량이 기하급수적으로 늘어난다는 문제점이 있다.
빅오 표기법으로 시간복잡도를 계산해보면, O(2^n)이기 때문에, f(100)을 호출한다면 연산횟수가 f(100) = 2^100 = 1,000,000,000,000,000,000,000,000,000,000번이다. 몇백시간을 기다려도 계산이 끝나지 않을 것이다.
2의 45승만큼의 연산만 해도 소요시간이 약 14초는 되는 걸 직접 확인해볼 수 있다.
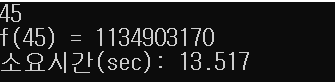
그런데 내가 당장 f(100)을 연산하는 프로그램을 구현하고 싶다고 할 때,
Dynamic Programming 기법을 이용하면 훨씬 적은 연산 횟수로 답을 도출할 수 있게 코드를 짤 수 있다.
피보나치 수열은 같은 계산이 반복되는 형태이기 때문에 아래 두 조건을 만족한다!
1) 큰 문제를 작은 문제로 나눌 수 있는가? -> Yes
2) 작은 문제에서 구한 정답이 그것을 포함하는 큰 문제에도 동일하게 적용되는가? -> Yes
즉, 아래와 같이 가지치기하며 반복되는 연산들을 계속 반복하게 하지 말고,
이미 계산된 f(k)에 대해서 연산 결과를 저장해놓았다가 재활용하는 것이다. 해당 방식대로 코드를 구현해보자.
연산 결과를 저장하기 위한 메모리를 조금 더 써야하긴 하지만 절약할 수 있는 연산 횟수에 비하면 효율적인 선택이라고 생각한다.

Dynamic Programming 기법을 사용하면 아래 사진만큼 연산 횟수가 줄어든다.
이미 계산된 f(4), f(3), f(2)에 대한 결과 연산을 한번만 진행하면 그 결과를 가져다가 쓰면 되기 때문이다!

Dynamic Promgramming 방식으로 구현한 코드는 아래와 같다.
result[n] 배열의 초기값을 0으로 초기화 시켜놓고, result[n]!=0이 아닌 경우는 이미 저장된 계산 결과를
가져다 쓴다. 그리고 아직 계산되지 않은 f(n)에 대해서는 result[n] 배열에 결과를 저장한다.
작성된 코드는 아래와 같다.
#include <iostream>
#include <ctime>
using namespace std;
// Dynamic Programming 방식으로 구현
int fibonacci(int n, long long* result) {
if (n == 1 or n == 2) {
return 1;
}
else if (result[n] != 0) {
return result[n];
}
else {
result[n] = fibonacci(n - 1, result) + fibonacci(n - 2, result);
return fibonacci(n - 1, result) + fibonacci(n - 2, result);
}
}
int main(void) {
// 시간 측정용
clock_t start, finish;
double duration;
int n;
cin >> n;
long long* result = new long long[n+1]{0, };
start = clock();
int answer = fibonacci(n, result);
finish = clock();
duration = (double)(finish - start) / CLOCKS_PER_SEC;
cout << "f(" << n << ") = " << answer << endl;
cout << "소요시간(sec): " << duration << endl;
return 0;
}
아까 약 13.5초가 걸렸었던 f(45) 연산을 수정된 코드로 다시 실행해보니 0(sec)로 연산 시간이 아주 많이 단축된 것을 확인할 수 있다. 연산 수행 횟수를 빅오표기법으로 다시 계산해보면, Dynamic Programming의 경우는 O(n)이다.
왜냐면 f(1) 구한 후 그 다음 값이 f(2)를 푸는데 사용되고 f(2)가 f(3)을 푸는데 사용되고..... 이러한 방식으로 이어지기 때문이다. 한번 구한 결과는 다시 구해지지 않는다. 피보나치 수열을 구하는 위 도식을 보면 직관적으로 이해할 수 있다.

vs

'백준' 카테고리의 다른 글
| Algorithm 개념정리: Greedy Algorithm (0) | 2025.01.15 |
|---|---|
| 백준 1541: 잃어버린 괄호 (0) | 2024.03.18 |
| 1931: 회의실 배정 (0) | 2024.03.17 |
| 백준 1744: 수 묶기 (0) | 2024.03.14 |
| 백준 1715: 카드 정렬하기 (0) | 2024.03.13 |



