📃 문제: 백준 6064_카잉 달력
https://www.acmicpc.net/problem/6064
M과 N보다 작거나 같은 두 개의 자연수 x, y를 가지고 각 년도를 <x:y>와 같은 형식으로 표현한다. 이 세상의 시초에 해당하는 첫 번째 해를 <1:1>로 표현하고, 두 번째 해를 <2:2>로 표현한다. <x:y>의 다음 해를 표현한 것을 <x':y'>이라고 하자. 만일 x < M 이면 x' = x + 1이고, 그렇지 않으면 x' = 1이다.
같은 방식으로 만일 y < N이면 y' = y + 1이고, 그렇지 않으면 y' = 1이다. <M:N>은 그들 달력의 마지막 해로 판단한다.
예를 들어, M = 10 이고 N = 12라고 하자. 첫 번째 해는 <1:1>로 표현되고, 11번째 해는 <1:11>로 표현된다. <3:1>은 13번째 해를 나타내고, <10:12>는 마지막인 60번째 해를 나타낸다.
네 개의 정수 M, N, x와 y가 주어질 때, <M:N>이 카잉 달력의 마지막 해라고 하면 <x:y>는 몇 번째 해를 나타내는지 구하는 프로그램을 작성하라.
예제 입력)
3
10 12 3 9
10 12 7 2
13 11 5 6
예제 출력)
33
-1
83
🥈 난이도: 실버 1
😲 사용한 개념: 유클리드 호제법, 수학, 부르트포스
☝️ 유클리드 호제법이란?
유클리드 호제법은 두 수의 최대공약수를 구하는 알고리즘이다.
(호제법 = 두 수가 서로 상대방의 수를 나누어서 결국 원하는 수를 얻는 알고리즘)
유클리드 호제법으로 최대공약수를 구하는 방법에 대해 알아보자.
먼저, 큰 수를 작은 수로 나눈 나머지를 구한다.(=MOD 연산 수행)
그 다음에, 나눴던 수와 나머지로 또 MOD 연산을 한다.
이 과정을 MOD 연산의 결과가 0이 될 때까지 반복한다.
나머지가 0이 되었을 때, 마지막 계산에서 나누는 수로 사용된 수가 입력받은 처음 두 수의 최대공약수가 된다!
간단하게 말하면, 유클리드 호제법은 MOD 연산을 반복하면 된다.
아래 그림을 참고해서 몇번 계산을 해보면 감이 올 것이다.
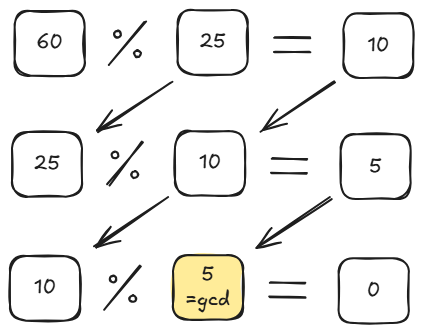
이를 소스코드로는 아래와 같이 구현할 수 있다.
// 최대공약수 구하기
int gcd(int a, int b) {
int c = a % b;
while (c != 0) {
a = b;
b = c;
c = a % b;
}
return b;
}
최소공배수의 경우는 직관적으로 (두 수의 곱) / (두 수의 최대공약수)를 구하면 그게 바로 최소 공배수가 될 것이다.
//최소공배수 구하기
int lcm(int a, int b) {
return (a * b) / gcd(a, b);
}
📖 풀이 사고 과정
위 '카이 달력' 문제의 조건을 잘 이해하고, 유클리드 호제법의 개념을 알고 있다면 어렵지 않게 해결할 수 있는 문제이다.
달력의 각 X, Y는 M과 N을 주기로 순회한다.
예를 들어 M = 12, N = 11이라면
X: 1 -> 2-> 3-> ... ->12 -> 1 -> 2 -> ...
Y: 1 -> 2-> 3-> ... ->11 -> 1 -> 2 -> ...
이런식으로 날짜가 순회할것이다.
이때 M과 N의 최소공배수가 되는 지점에서 날짜가 다시 <1, 1> (=시작지점)으로 돌아올 것이고, 같은 패턴을 반복하며 날짜 지나갈 것이다.
따라서 특정 <x, y>일이되는 일수를 찾기 위해서는 M과 Y의 최소공배수만큼까지 탐색을 해보면 가능한 날짜인지 아닌지와, 해당 날짜에 도달하기 위해서 몇일이 지나야 하는지를 구할 수 있다.
즉,
1) M, N의 최소공배수를 구하고,
2)최소공배수에 해당하는 일수만큼 순회하면서 (i % M) == X && (i % N) == Y 조건을 만족하는 일 수를 구하면
문제를 해결할 수 있다.
👩💻 구현 코드(c++ 사용)
#include <iostream>
#include <vector>
using namespace std;
// 최대공약수 구하기
int gcd(int a, int b) {
int c = a % b;
while (c != 0) {
a = b;
b = c;
c = a % b;
}
return b;
}
//최소공배수 구하기
int lcm(int a, int b) {
return (a * b) / gcd(a, b);
}
int calculateDate(int M, int N, int X, int Y) {
int lcmResult, result = -1;
// 1) M, N의 최소공배수 구하기
lcmResult = lcm(M, N);
// 2) x, y가 몇번째 해인지 구하기
result = -1;
for (int i = X; i <= lcmResult; i++) {
if (i % M == X && i % N == Y) {
result = i;
break;
}
}
for (int i = X; i <= lcmResult; i +=M) {
if (i % N == Y % N) {
result = i;
break;
}
}
return result;
}
int main(void) {
int n, M, N, X, Y;
vector<int> answerList;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> M >> N >> X >> Y;
int result = calculateDate(M, N, X, Y);
answerList.push_back(result);
}
for (int answer : answerList) {
cout << answer << endl;
}
return 0;
}원래는
조건) i = X부터 lcmResult까지 1씩 증가하면서 반복한다.
목적) i % M == X 그리고 i % N == Y를 동시에 만족하는 값을 찾는다.
이 때,
i % M == X 조건이 있기 때문에, 사실상 i는 X와 같은 나머지를 갖는 M의 배수로 제한된다.
-> 이 조건만으로도 i의 후보는 X, X+M, X+2M, ...로 한정된다.
그렇기 때문에 M과 N의 최소공배수만큼의 일수를 일일히 순회하지 않고, 반복문의 효율을 높이기 위해서
i = X부터 시작하지만, 이번에는 M씩 증가하도록 소스코드를 작성하였다.
결론적으로,
이미 i는 X와 같은 나머지를 갖는 M의 배수이므로, 첫 번째 코드의 i % M == X 조건이 자동으로 만족된다.
따라서 두 번째 코드에서는 굳이 i % M == X를 체크할 필요 없이, i % N == Y만 확인하면 된다.
이때 Y%N은 Y>N이 될 경우를 방지하기 위함이다.